We give a quick tour through some topics in analytic prime number theory, focusing in particular on the strange mixture of order and chaos in the primes. For instance, while primes do obey some obvious patterns
(e.g. they are almost all odd), and have a very regular asymptotic distribution (the prime number theorem), we still do not know a deterministic formula to quickly generate large numbers guaranteed to be prime, or to count even very simple patterns in the primes, such as twin primes p, p+2. Nevertheless, it is still possible in some cases to understand enough of the structure and randomness of the primes to obtain some quite nontrivial results.
Introduction
The prime numbers 2, 3, 5, 7, . . . are one of the oldest topics studied in mathematics. We now have a lot of intuition as to how the primes should behave, and a great deal of confidence in our conjectures about the primes... but we still have a great deal of difficulty in proving many of these conjectures! Ultimately, this is because the primes are believed to behave pseudorandomly in many ways, and not to follow any simple pattern. We have many ways of establishing that a pattern exists... but how does one demonstrate the absence of a pattern?
This article will try to convince you why the primes are believed to behave pseudorandomly, and how one could try to make this intuition rigorous. This is only a small sample of what is going on in the subject; many major topics are omitted, such as sieve theory or exponential sums, and am glossing over many important technical details.
Finding Primes
It is a paradoxical fact that the primes are simultaneously very numerous, and hard to find. On the one hand, we have the following ancient theorem:
Theorem 1 (Euclid’s Theorem). There are infinitely many primes. In particular, given any k, there exists a prime with at least k digits. But there is no known quick and deterministic way to locate such a prime! (Here, “quick” means “computable in a time which is polynomial in k”.) In particular, there is no known (deterministic) formula that can quickly generate large numbers that are guaranteed to be prime.
On the other hand, one can find primes quickly by probabilistic methods. Indeed, any k-digit number can be tested for primality quickly, either by probabilistic methods or by deterministic methods. These methods are based on variants of Fermat’s little theorem, which asserts that a^n ≡ a mod n whenever n is prime. (Note that an mod n can be computed quickly, by first repeatedly squaring a to compute a^2^j mod n for various values of j, and then expanding n in binary and multiplying the indicated residues a^2^j mod n together.)
Also, we have the following fundamental theorem:
Theorem 2 (Prime Number Theorem). The number of primes less than a given integer n is
Is Randomness Really Necessary? To summarize: We do not know a quick way to find primes deterministically. However, we have quick ways to find primes randomly. On the other hand, there are major conjectures in complexity theory, such as P = BPP, which assert (roughly speaking) that any problem that can
be solved quickly by probabilistic methods can also be solved quickly by deterministic methods.
These conjectures are closely related to the more famous conjecture P = NP, which is a USD $ 1 million Clay Millennium prize problem. Many other important probabilistic algorithms have been derandomised into deterministic ones, but this has not been done for the problem of finding primes.
Counting Primes
We have seen that it’s hard to get a hold of any single large prime. But it is easier to study the set of primes collectively rather than one at a time.
An analogy: it is difficult to locate and count all the grains of sand in a box, but one can get an estimate on this count by weighing the box, subtracting the weight of the empty box, and dividing by the average weight of a grain of sand. The point is that there is an easily measured statistic (the weight of the box with the sand) which reflects the collective behaviour of the sand. For instance, from the fundamental theorem of arithmetic one can establish Euler’s product formula
for any s > 1 (and also for other complex values of s, if one defines one’s terms carefully enough).
The formula (1) links the collective behaviour of the primes to the behaviour of the Riemann zeta function
thus 
thus One can then deduce information about the primes from information about the zeta function (and in particular, its zeroes).
In a similar spirit, one can use the techniques of complex analysis, combined with the (non-trivial) fact that ζ(s) is never zero for s ∈ C when Re(s) ≥ 1, to establish the prime number theorem; indeed, this is how the theorem was originally proved (and one can conversely use the prime number theorem to deduce the fact about the zeroes of ζ).
The famous Riemann hypothesis asserts that ζ(s) is never zero when Re(s) > 1/2. It implies a much stronger version of the prime number theorem, namely that the number of primes less than an integer n > 1 is given by
the more precise formula
is a quantity which is bounded in magnitude by Cn1/2 log n for some absolute constant C (for instance, one can take C = 1/8π once n is at least 2657).
The hypothesis has many other consequences in number theory; it is another of the USD $ 1 million Clay Millennium prize problems. More generally, much of what we know about the primes has come from an extensive study of the properties of the Riemann zeta function and its relatives, although there are
also some questions about primes that remain out of reach even assuming strong conjectures such as the Riemann hypothesis.
Modeling Primes
A fruitful way to think about the set of primes is as a pseudorandom set — a set of numbers which is not actually random, but behaves like one.
For instance, the prime number theorem asserts, roughly speaking, that a randomly chosen large integer n has a probability of about 1/ log n of being prime. One can then model the set of primes by replacing them with a random set of integers, in which each integer n > 1 is selected with an independent probability of 1/ log n; this is Cram´er’s random model.
This model is too crude, because it misses some obvious structure in the primes, such as the fact that most primes are odd. But one can improve the model to address this, by picking a model where odd integers n are selected with an independent probability of 2/ log n and even integers are selected with probability 0.
One can also take into account other obvious structure in the primes, such as the fact that most primes are not divisible by 3, not divisible by 5, etc. This leads to fancier random models which we believe to accurately predict the asymptotic behaviour of primes.
For example, suppose we want to predict the number of twin primes n, n + 2, where n ≤ N for a given threshold N. Using the Cram´er random model, we expect, for any given n, that n, n+2 will simultaneously be prime with probability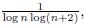
so we expect the number of twin primes to be about
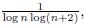so we expect the number of twin primes to be about
This prediction is inaccurate; for instance, the same argument would also predict plenty of pairs of consecutive primes n, n+1, which is absurd. But if one uses the refined model where odd integers n are prime with an independent probability of 2/ log n and even integers are prime with probability 0, one gets the slightly different prediction
More generally, if one assumes that all numbers n divisible by some prime less than a small threshold w are prime with probability zero, and are prime with a probability of 
otherwise, one is eventually led to the prediction
otherwise, one is eventually led to the prediction
(for p an odd prime, among p consecutive integers, only p −2 have a chance to be the smaller number in a pair of twin primes). Sending w →∞, one is led to the asymptotic prediction
Similar arguments based on random models give convincing heuristic support for many other conjectures in number theory, and are backed up by extensive numerical calculations.
Finding Patterns in Primes
Of course, the primes are a deterministic set of integers, not a random one, so the predictions given by random models are not rigorous. But can they be made so?
There has been some progress in doing this. One approach is to try to classify all the possible ways in which a set could fail to be pseudorandom (i.e. it does something noticeably different from what a random set would
do), and then show that the primes do not behave in any of these ways. For instance, consider the odd Goldbach conjecture: every odd integer larger than five is the sum of three primes. If, for instance, all large primes happened to have their last digit equal to one, then Goldbach’s conjecture could well fail for some large odd integers whose last digit was different from three. Thus we see that the conjecture could fail if there was a sufficiently strange “conspiracy” among the primes.
However, one can rule out this particular conspiracy by using the prime number theorem in arithmetic progressions, which tells us that (among other things) there are many primes whose last digit is different from 1. (The proof of this theorem is based on the proof of the classical prime number theorem.) Moreover, by using the techniques of Fourier analysis (or more precisely, the Hardy-Littlewood circle method), we can show that all the conspiracies which could conceivably sink Goldbach’s conjecture (for large integers, at
least) are broadly of this type: an unexpected “bias” for the primes to prefer one remainder modulo 10 (or modulo another base, which need not be an integer), over another.
Vinogradov eliminated each of these potential conspiracies, and established Vinogradov’s theorem: every sufficiently large odd integer is the sum of three primes.This method has since been extended by many authors, to cover many other types of patterns; for instance, related techniques were used by Ben Green and myself to establish that the primes contain arbitrarily long arithmetic progressions, and in subsequent work of Ben Green, Terence Tao, and Tamar Ziegler to count a wide range of other additive patterns also. (Very roughly speaking, known techniques can count additive patterns that involve two independent parameters, such as arithmetic progressions a, a + r, . . . , a + (k − 1)r of a fixed length k.)
Unfortunately, “one-parameter” patterns, such as twins n, n + 2, remain stubbornly beyond current technology. There is still much to be done in the subject!
Alfore is a reluctant blogger, a lazy poet, and a great daydreamer. He owns a Nobel, Pulitzer, Oscar and a bunch of weirdly named cats.
View My Complete Profile
0 comments:
Post a Comment